Vi kan ikke gå i noen detalj om hvordan musikkinstrumentene fungerer her, men det er viktig å forstå eksitator-resonator-modellen som gir en viss forståelse av mange forskjellige instrumenter.
Når vi klimprer en gitarstreng med lengde L meter, vil det forplante seg en bølge til begge sider i strengen. Denne bølgen reflekteres i endene, og farer fram og tilbake. Vi får dermed en svingning som kunne ha vart til evig tid, hvis det ikke var for at friksjonen demper bevegelsene etterhvert.
Hva slags svingninger kan vi så få? Siden strengen er spikret fast
i endene, må det kreves at posisjonen her er null, og dessuten at strengen
står stille her.
![]() Dette gir såkalte stående bølger. Strengens form på
ethvert tidspunkt kan beskrives som en sum av sinusoider.
Dette gir såkalte stående bølger. Strengens form på
ethvert tidspunkt kan beskrives som en sum av sinusoider.
![]() Den første mulige sinusoiden som er null i begge ender, har bølgelengde
lik to ganger strengens lengde (
Den første mulige sinusoiden som er null i begge ender, har bølgelengde
lik to ganger strengens lengde ( ![]() ), og vi får en bevegelse
opp og ned overalt på strengen, men mest på midten (figur 3.12).
), og vi får en bevegelse
opp og ned overalt på strengen, men mest på midten (figur 3.12).
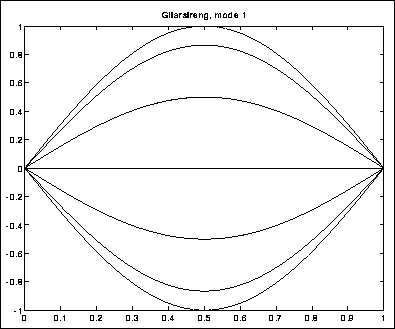
Figure 3.12: Grunnsvingning på gitarstreng
Dette er en halv sinusbølge, og denne halvdelen har altså en
lengde ![]() . Det er derfor vi har at
. Det er derfor vi har at ![]() .
.
Hvilken frekvens vi får, vil foruten bølgelengden avhenge av
lydhastigheten gjennom strengen, som igjen avhenger av strengens
tykkelse, masse og stivhet. Sammenhengen mellom frekvens, fart og
bølgelengde er ![]() .
.
Den andre mulige sinusoiden har bølgelengde lik strengens lengde
( ![]() ) og vi får en bevegelse opp og ned med en
stillestående knute på midten (figur 3.13).
) og vi får en bevegelse opp og ned med en
stillestående knute på midten (figur 3.13).
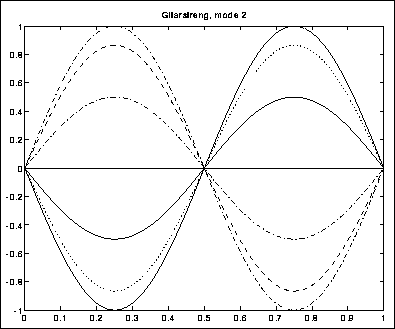
Figure 3.13: Første overtone på gitarstreng
Siden bølgelengden her er halvparten av den over, vil denne svingningen ha dobbelt så høy frekvens.
Vi kan også ha svingninger med bølgelengde lik halvparten av strengelengden, en tredel osv. Disse bølgelengdene vil gi en grunnfrekvens (mode 1) med overtoner (mode 2, 3 etc.). Alle disse svingningene vil være tilstede på en gang, og summere seg sammen til et helt spektrum med grunntone og overtoner. Hvis strengens lengde varierer, vil bølgelengdene variere tilsvarende, og vi får ulike grunnfrekvenser.
Spekteret fra strengen farges videre av gitarkassen, som virker som et filter med forskjellige resonanser, dvs. at visse frekvensområder framheves.
I dette tilfellet kan vi kalle strengen for en eksitator (lydprodusent), og gitarkassen for en resonator.
Etter at vi har klimpret en gitarstreng svinger den fritt. På en fiolin derimot, opprettholdes svingningen av buens bevegelse. Dette kan vi kalle tvungen svingning (forced vibration). Denne mekanismen fungerer ved at friksjonen mellom buen og strengen gjør at strengen dras med buen et lite stykke. På et visst tidspunkt blir imidlertid motkraften for stor, og strengen spretter momentant tilbake. Så tar buen tak i strengen igjen, og prosessen gjentar seg. Fysikere kaller denne prosessen for slip and grip. Vi får dermed en slags sagtannkurve (figur 3.14).
Vi får samme type svingning når vi f.eks. drar et bord bortover gulvet. Den fryktede skrikingen av kritt mot tavle er et annet eksempel.
Som for gitaren, vil strengen ha visse frekvenser (grunntone og overtoner) som det er mulig for den å svinge på. Det er viktig at frekvensen til sagtannkurven faller sammen med en slik naturlig frekvens. Det ville vært en håpløs oppgave for fiolinisten å måtte tilpasse frekvensene manuelt. Heldigvis skjer det en tilbakekobling (feedback) fra strengen til buen, som gjør at de to frekvensene låses til hverandre helt av seg selv.
Hvis en trykkbølge farer fram og tilbake i et rør som er lukket i den ene enden og åpent i den andre, vil det settes opp en stående bølge. Vi får null utsving (knute) i luftttrykket i den åpne enden, og maksimalt utsving i den lukkede enden. Som vist i figur 3.15, der den åpne enden er til venstre, gir dette modus 1 (grunntonen).
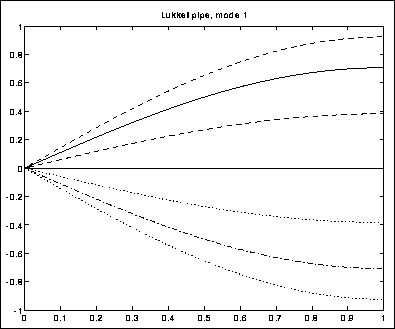
Figure 3.15: Grunnsvingningen i en pipe med en lukket og en åpen
ende
Hvis røret er L meter langt, ser vi at bølgelengden til
grunntonen er ![]() meter. Fra sammenhengen mellom frekvens, fart og
bølgelengde (
meter. Fra sammenhengen mellom frekvens, fart og
bølgelengde ( ![]() ) får vi frekvensen til
grunntonen, f.eks. for et 140 cm langt rør:
) får vi frekvensen til
grunntonen, f.eks. for et 140 cm langt rør:
![]()
Neste mulige stående bølge er vist i figur 3.16.
Bølgelengden er her ![]() , som gir frekvensen
, som gir frekvensen
![]()
Videre vil vi kunne få svingninger med frekvens ![]() ,
,
![]() etc.
Vi ser at vi får et spektrum med bare odde overtoner.
etc.
Vi ser at vi får et spektrum med bare odde overtoner.
Parasaurolophus
Andeøglene (hadrosaurene) er en gruppe dinosaurer fra Kritt-tiden. Mange andeøgler har en underlig "hjelm" på hodet, som inneholder lange rør av bein. Mange rare forklaringer ble gitt på dette tidligere. Det var f.eks. en vanlig misforståelse at disse svære dyrene levde i vann, og at hode-apparatet ble brukt som luft-reservoar eller snorkel.
Det er nå klarlagt at det dreier seg om et akustisk apparat, en resonator som hjalp til i produksjonen av brøl og støt som må ha vært helt fantastiske. Et eksempel er Parasaurolophus, som hadde en lang kam på hodet, hvor to parallelle piper var kveilet dobbelt. Pipene begynner nede i halsen (lukket ende), hvor det formodentlig satt en slags eksitator. Det finnes noen skrå beinflater som minner mistenkelig om dem vi finner i orgelpiper, så kanskje dyret bare blåste luft fra sine digre lunger. Pipene endte i hvert sitt nesebor (åpen ende), men det er ikke funnet noe som likner på sjalstykker. Den amerikanske paleontologen Jim Bakker har laget en plastmodell som man kan bruke som blåseinstrument, og det pågår arbeid med digital fysisk modellering for å syntetisere lyden.
Lengden på hver pipe er tilsammen ca. 2.4 meter,
![]() og ut fra dette kan vi regne ut frekvensen til grunntonen:
og ut fra dette kan vi regne ut frekvensen til grunntonen:
![]()
Dette er virkelig en lav frekvens, og det betyr at lyden bar langt. Dagens elefanter kommuniserer også på svært lave frekvenser, tildels under menneskets hørbare område (subsonisk lyd eller infralyd).
Et trompet er ikke et enkelt rør, og dette gir betydelige endringer
sammenliknet med situasjonen over. Et komplisert samspill mellom
munnstykke, rør og sjalstykke medfører at vi får resonanser
for ![]() ,
, ![]() ,
, ![]() etc. Vanlig dyp tone (med alle ventiler
åpne) for en messingblåser har grunntonen på
etc. Vanlig dyp tone (med alle ventiler
åpne) for en messingblåser har grunntonen på ![]() , og
overtonene på
, og
overtonene på ![]() ,
, ![]() etc. En trompet har et ca. 140 cm
langt rør, og dette skulle gi en
etc. En trompet har et ca. 140 cm
langt rør, og dette skulle gi en ![]() på 61 Hz, og dermed
grunntone
på 61 Hz, og dermed
grunntone ![]() =244 Hz. Dette er omtrent hva man observerer.
=244 Hz. Dette er omtrent hva man observerer.
Når man spiller en trompet, vil svingningene fra leppene (eksitator) synkroniseres med frekvensen til en av de mulige svingningsmodi, akkurat som vi så for fiolinen. Dette gjør at det er nærmest umulig å spille toner mellom de som er gitt fra rørets lengde. For å utvide antallet tilgjengelige noter, kan man endre rørlengden med ventiler eller glidende rør (trombone).
Sjalstykket ("tuten") fungerer som en pussig resonator, som former spekteret videre.
Menneskestemmen kan også innpasses i eksitator-resonator-modellen.
Eksitator er stemmebåndene, som sitter i strupehodet (glottis).
Disse svinger med et meget rikt overtonespektrum. Grunnfrekvensen
styres først og fremst av strammimngen av stemmebåndene, men
lengden på røret
over strupehodet spiller også inn. Hvis man synger en lys tone,
vil strupehodet plassere seg høyt oppe i halsen. Når man går
ned i tonehøyde, vil man tydelig kunne se at strupehodet faller langt
nedover. Hastigheten lyden forplanter seg med i røret er også
viktig, fordi ![]() . Hvis man fyller rommet over
glottis med helium, vil lyden gå fortere og tonehøyden vil øke.
. Hvis man fyller rommet over
glottis med helium, vil lyden gå fortere og tonehøyden vil øke.
Når man hvisker, blåser man bare luft istedet for å lage en svingning med en grunnfrekvens. Like over glottis vil vi da ha hvit støy, dvs. at alle frekvenser er like sterkt til stede i et kontinuerlig spektrum.
Enten man snakker eller hvisker, vil luftrøret over glottis, samt munnhulen, fungere som et filter (resonator) som farger det rike spekteret fra glottis på ulike måter avhengig av hvordan vi former munnhulen. På den måten oppstår de ulike vokalene.